Kvadratiske likninger i 1T

I et tidligere innlegg har jeg skrevet noen tanker om elevens møte med de kvadratiske likningene i Matematikk 1T. For nye lesere som måtte være interessert vil jeg dele mitt opplegg på ny.

Tanken bak opplegget er at jeg ønsker at elevene skal forstå hva som skjer når vi løser andregradslikninger (og ikke bare bruke en formel). Lærebøkene gjør ikke en god jobb her. Det blir kun instrumentell forståelse. Jeg vil at elevene skal forstå hvordan vi fullfører et kvadrat.

Her kan du laste ned en pdf-fil av opplegget.

Bruk det om du vil. ;-)

Matematisk tekst i Itslearning

Det hender ofte at jeg må svare på sprørsmål fra elever på meldingssystemet til Itslearning. Desverre er det ikke noen god formeleditor i Itslearning. Derfor pleier jeg ofte å svar på formen

f’(x)=(x^2-2x)/(x-1)^2

Dette ser jo ikke særlig pent ut. Men så leket jeg litt med MathType (som alle i videregående skole i Hordaland fylkeskommune har lisens på) og test litt med ulike innstillinger. Her er hva jeg ente opp med:

For å få til dette har jeg endret «Cut and Copy Preferences» som vist under:

 

Når dette er gjort er det bare til å skrive inn den matematiske teksten, markere og kopiere og lime inn. Dessverre fungerer dette ikke så bra om du bruker Internett Explorer (som jeg ikke kunne tenke meg å gjøre…). Slik vil matematikken da kunne se ut:

Geometri i Matematikk R1

I år underviser jeg blant annet i R1. Der er et av temaene geometri. Hvorfor har vi egentlig fått geometri inn i læreplanen vår? Hva er tanken med at elevene skal sitte å drive på med ulike konstruksjoner med passer og linjal? Dette er noe de sannsynligvis aldri mer vil gjøre! Hva er poenget?

I læreplanen kan vi blant annet lese følgende om hva elevene skal kunne:

• bruke linjer og sirkler som geometriske steder sammen med formlikhet og setningen om periferivinkler i geometriske resonnementer og beregninger
• utføre og analysere konstruksjoner definert av rette linjer, trekanter og sirkler i planet, med og uten bruk av dynamisk programvare

Dette er et tema jeg synes er veldig gøy! Det er en del geometri i ungdomsskolen. Der har elevene gjort ulike konstruksjoner og muligens også lært litt om Thales setning. Hva er så nytt i R1? Slik jeg ser det tolker lærebokforfatterne kompetansemåla over som at det er stort sett det samme som de driver på med i ungdomsskolen, bare nå kan vi introdusere periferivinkelsatsen og ta dette med formlikhet og kongruens litt grundigere. Men dette synes jeg er trist! I formålet med faget kan vi lese at

Arbeid med programfaget skal gi en innføring i logisk og analytisk tankegang med vekt på matematisk argumentasjon og framstillingsform,…

I beskrivelsen av den grunnleggende ferdigheten å kunne uttrykke set muntlig og skriftlig står det:

Å kunne uttrykke seg muntlig og skriftlig i matematikk for realfag innebærer å formulere logiske resonnementer,…

Jeg har ofte hørt at poenget med geometrien er at elevene skal lære seg å være nøyaktige. Da er tanken at det blir mye mer nøyaktig å konstruere enn 60 graders vinkel enn å tegne den med gradskive. Dette er jeg totalt uenig i! Ut fra erfaring som lærer i ungdomsskole, videregående og høyskole kan jeg si at jeg aldri har sett noen tegne mer nøyaktig en 60 graders vinjkel med passer og linjal enn de kan med en gradskive! Så hva er da poenget? Er det ikke at elevene må gjøre alle disse resonnementene? De må planlegge en konstruksjon og kunne argumentere for at den faktisk gir det søkte geometriske sted!

Men nå er vi i videregående og R1. Her burde vi ha fokusert litt mer på geometriens oppbygning og struktur. Det er en katastrofe at Euklid er så og si fraværende i lærebøkene. Selv om dette er vanskelige tema, så synes jeg at vi skylder elevene å gi de et visst innblikk i hvordan matematikk er bygd opp på aksiomer og grunnleggende objekter.

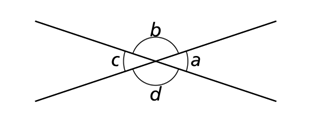
La meg ta et eksempel. Bevis at toppvinklene til to linjer som krysser hverandre er like. Det vil si: vis at a=c og b=d i figuren under.

Dette er et problem som jeg kan huske at vi jobbet med i 9. klasse. Vi ser at b+c=90° og a+b=90°. Dette gir oss at a=c. Tilsvarende vises b=d. Men hvilke forutsetninger gjør vi når vi gjennomfører dette beviset?

Jeg pleier alltid å introdusere elevene til Euklid og hans fem postulater. Disse er:

1. Det er alltid mulig å trekke en rett linje mellom to punkter
2. Det er alltid mulig å forlenge en endelig, rett linje til en uendelig, rett linje
3. Det er mulig å beskrive en sirkel med et hvilke som helst sentrum og en hvilke som helst distanse (radius)
4. Alle rette vinkler er like (90°)
5. Anta at en rett linje krysser to rette linjer. Anta videreat dette skjer slik at de to indre vinklene er mindre ennto rette vinkler. Hvis de rette linjene forlenges, vil de skjære hverandre i et punkt på den siden der summen av de indre vinklene er mindre enn to rette vinkler.

Hvilke av disse postulatene brukte jeg i resonnenementet over?

Et annet standard ekesmpel er beviset for at summen av vinklene i en trekant er 180°. Figuren øverst i dette blogginnlegget illustrerer et bevis for denne påstanden. Men hvilke av de dem postulatene brukes i beviset?

Poenget er at elevene skal se at vi må ha noen grunnleggende og «opplagte» byggesteiner å bygge videre mer. For meg er det viktig å introdusere elevene for denne siden av matematikken. Og for ordens skyld: du kan aldri bevise noe med GeoGebra!

Får de dette på eksamen? Til dette vil jeg svare at all undervisning skal ikke være rettet inn mot eksamen!

Til slutt to gåter:

En bjørn gikk 10 km sørover, deretter 10 km østover og deretter 10 km nordover. Da var han på samme plass som han startet. Hvilken farge har bjørnen?

En fugl flyttet seg 10 km sørover, 10 km østover og 10 km nordover. Hvilke farger hadde fuglen?