Med bærbar pc på pulten har elevene større tilgang på digitale hjelpemidler enn med en vanlig kalkulator. På vår skole bruker vi følgende programmer i undervisningen: Excel, GeoGebra og wxMaxima. Foruten disse har også elevene kalkulator – de fleste en grafisk kalkulator.
I dette blogginnlegget vil jeg reflektere litt over bruken av slike verkøtøyprogram i forhold til elevenes læring av matematikk. Jeg vil ta for meg programmet wxMaxima og se på noen eksempler som belyser ulike utfordringer knyttet til ulike oppgavetyper elevene jobber med.
wxMaxima er et symbolmanipulerende verktøy. Det innebærer at du med dette kan finne eksakte løsninger på ulike oppgaver. Vil du løse liknikngen $x^3-2x+1=0$? Ingen problem. Du skriver likningen inn i programmet og klikker på OK og vips så får du ut de tre eksakte røttene: $x=1,x=-\frac{\sqrt{5}+1}{2} , x= \frac{\sqrt{5}-1}{2}$
Hva har så dette med matematikk å gjøre? Svaret er ganske enkelt: ingen ting! Men dette betyr ikke at slike digitale verktøy er meningsløse i matematikklæring. Tverrt om! Poenget er at slike verktøy ikke er hensiktsmessige i elevens matematikklæring når det gjelder slike typer oppgaver. Jeg bruker en hovedregel i min undervisning at før elevene får bruke slike digitale vertøy i deres arbeid med matematikken, så skal de først ha jobbet med fagstoffet for hånd. I videregående har vi nå todelt eksamen, så det vektlegges at elevene skal kunne løse ulike oppgaver uten hjelpemidler. Det er først når dette er på plass at de digitale vertøyene tilbys. Så da blir det naturlige spøsrmålet: hvorfor det? Hvofor i det hele tatt tilby elevene slike vertøy?
Vi kan dele bruke av IKT i matematikkfaget i to grove kategorier:
- IKT som forenkler. Vi kan bruke IKT til å fornkle ulike oppgaver slik at vi slipper å bruke så mye tid til tekniske detaljer.
- IKT til nyskaping. Vi kan bruke digitale vertøy til nye typer oppgaver på en måte som ikke er mulig uten digitale vertøy.
I R2 skal elevene regne ut vektorprodukt til vektorer i rommet. Dette er litt styr og det er lett å gjøre en slurvefeil. Formelen for et slik produkt er $ [u_1, u_2, u_3]\times [v_1, v_2, v_3 = [u_2v_3-u_3v_2, u_3v_1-u_1v_3, u_1v_2-u_2v_1]$
Her kan det regnes som en velsignelse å kunne skrive dette inn i wxMaxima og få svaret rett ut:

Hva så med den andre kategorien? Kan det tenkes at vi kan bruke digitale vektøy på nye typer oppgaver til elevene? Dette er en stor utfordring for matematikklærere! Hvilke oppgaver passer til våre elever? Hvor finner vi de ulike oppgavene? Hvordan jobbe med elevene? Jeg ser at følgende oppgave ofte blir gitt når elevne skal bruke digitale verktøy på i matematikkunderviningen:
La f være en tredjegradsfunksjon som har tre nullpunkter. Velg to nullpunkt og la T være tangenten til f i x lik middelverdien til de to nullpunktene. Hva kan du si om denne tangenten?
Her er vi ute etter Lorents Bies setning som sier at tangenten vil gå gjennom det tredje nullpunktet.
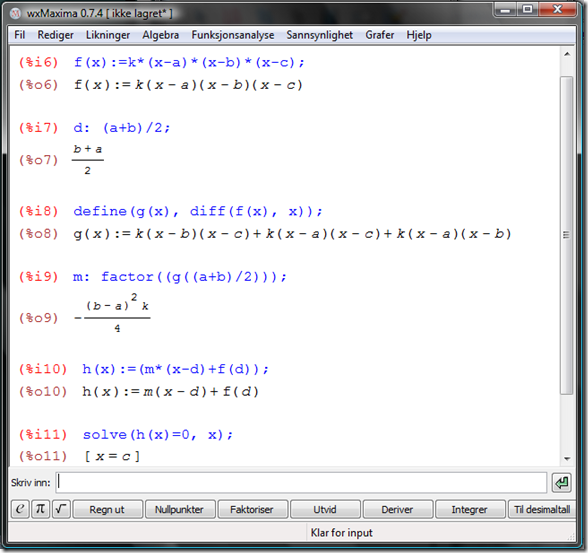
Å oppdage denne sammenhengen er en ting. Dette synes jeg er lettest å gjøre i GeoGebra. Men å vise det generelt er en annen ting. Dette krever en annen form for matematisk kompetanse enn å løse ferdig oppstillte oppgaver. Ideelt sett er det en slik kompetanse vi vil at elevene skal få, ikke sant? Men dette er lettere sagt enn gjort. Med fare for å ødelegge de som måtte få denne oppgaven, så viser jeg her hvordan jeg har løst oppgaven generelt ved hjelp av wxMaxima:
Her vil jeg si at vi får bruk for symbolmanipuleringen på en god måte. Resultatet er bevist. Vi har startet med et tredjegradsspolynom med tre nullpunkt a, b og c. Vi ha valgt to av nullpunkta (a og b) og vi har funnet tangenten i ((a+b)/2, f((a+b)/2)) og funnet nullpunktet til denne til å være c. Men å gjøre dette er langt i fra lett! Kan vi egentlig kreve dette av en elev i videregående skole?
Problemet dukket opp på eksamen i R1 i vår. På oppave 4, alternativ II fikk elevene en oppgave som dreiede seg om to fjerdegradsfunksjoner. Elevene skal finne vendepunktene S og T til grafen, finne linja som går gjennom vendepunkta og finne de to andre skjæringspunkta P og Q mellom linja og grafen. Så skal de regne ut forholdet mellom ST og TQ, der Q er skjæringspunktet lengst til høyre.
I de to eksemplene elevene jobbet med, går det fram at forholdet blir det samme, nemlig det gyldne snitt. Her kunne det være interessant å vise dette generelt, noe jeg har gjort i et tidligere blogginnlegg. Men i sensorveildeningen står det at dette ikke kreves for full uttelling. Hvorfor? Fordi det er å kreve for mye av elevene…
Hvorfor er det slik? Morten Blomhøj har i sin forsking identisfisert tre måter elevene bruker digitale verktøy:
- Den usikre og defensive elevvirksomheten
- Den løsningsoriterte elevvirksomheten
- Den reflekterende elevvirksomheten
Den første elevvirksomheten kjennetegnes ved at elevene kun har en instrumentell forståelse av ferdighetene jf likningen tidlig i dette blogginnlegget. Det klikkes og trykkes og ut kommer svara. Blomhøj skriver i artikkelen Læringsvilkår i datamskinbasert matematikkundervisning (i Matematikk for skolen, Barbro Grevholm red.):
Eleven fokuserer på å utvikle en instrumentell og prosessoirentert forsåelse, men de mangler ofte en grunnleggende forståelse av de matematiske objektene de arbeider med.
Den løsningsorienterte virksomeheten dreier seg om ytre forbindelser til det faglige innholdet i oppgavene. Her er det ikke forståelse som er viktig, men det å kunne klare å finne det rette svaret. Denne elevvirksomheten skiller seg ut fra den første ved at elevene er i stand til å formidle svarene sine på en faglig relevant måte. Her brukes IKT som forenkler.
Den reflekterte elevvirksomheten kjennetegnes ved at elevene vurdere ulike løsningsmetoder og er fleksible i forhold til disse. De driver med det som Schoenfeld kaller for monitoring. De overvåker sin egen løsniongsprosess og stiller seg selv spørsmål som: «Fører dette fram til svaret?» og «Hvorfor gjør vi dette? Finnes det en letter måte?»
Blomhøj skriver videre i sin artikkel:
Hvis undervisningen skal kunne støtte utvikloingen av en reflekterende elevvirksomhet, er det helt åpenbart nødvendig at elevene arbeider tilstrekkelig ofte med problemløsing, det vil si at de beskjeftiger seg med oppgaver som de er interessert i å løse, men som de ikke kan løse umiddelbart ved å bruke en metode som er velkjent for dem.
Dette er jeg hjertens enig i. Men jeg synes det er veldig vanskelig å få dette til i undervisningen. Det er to utfordringer som jeg spesielt vil nevne: den ene er problemet med å finne gode oppgaver som egner seg på de ulike trinn. Det må være oppgaver som passer til læreplan og fagstoff. Det er min erfaring at dette er noe som de fleste strever med. Den andre utfordringen er at dette vil nødvendigvis ta tid. Jeg kjenner pensumpresset er ganske stort i videregående skole og jeg skulle ønske at læreplangruppa hadde kuttet i hvertfall et hovedemne…
Blomhøj skriver at vi ikke har noen grunn til å forvente at innføring av datamskiner vil gi noen rasjonaliseringsgevinst i forhold til elevenes innlæring av det vanlige faglige innholdet. Men de vil lære seg å bruke digitale verktøy…
Hva er så konklusjonen på et litt lengre enn vanlig blogginnlegg? Å innføre digitale verktøy innebærer en didaktisk utfordring for læreren. Ved tradisjonelle oppgaver er det viktig å la elevene jobbe uten digitale vertøy for så å innføre vertøyene på et senere tidspunkt. Vi ønsker ikke at elevene kun skal ha en instrumentell forståelse, men vil ha refleksjoner og forståelse. Vi må kanskje tenke gjennom en gang til hva det vil si å ha en matematisk kompetanse…?!?