Elevene har hatt eksamen i R1 i dag. På oppgave 4 er det to alternativer. Jeg tipper at de fleste elevene har valgt alternativ I, som går ut på å finne et polynom, derivere det, finne topp- og bunpunkter, ventepunkter etc.
Alternativ II derimot, dreier seg om to fjerdegradsfunksjoner. Elevene skal finne vendepunktene S og T til grafen, finne linja som går gjennom vendepunkta og finne de to andre skjæringspunkta P og Q mellom linja og grafen. Så skal de regne ut forholdet mellom ST og TQ, der Q er skjæringspunktet lengst til høyre.
Dette skal de gjøre for to slike funksjoner og kommentere resultatet. Hva er resultatet? Svaret blir det samme i begge tilfellene, nemlig det gyldne snitt.
Som en artig øvelse har jeg brukt TI-Interactive! til å løse problemet generelt. Jeg staret da med å definerer en generell tredjegradsfunksjon:
Dobbeltderiverer f(x):
Finner likningen for linja gjennom vendepunktene: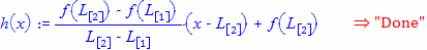
Finner de to andre skjæringspunktene mellom linja og f(x):
Dette går ikke, så jeg må finne på noe lurt. Deler vekk (x-L[1])(x-L[2)). Det vil si at jeg da får et andregradspolynom med de to andre x-koordinatoene til skjæringspunkta til h og f som nullpunkt:
Finner nullpunkene:
Regner så ut avstandene
Regner til slutt ut forholdet:
Hva ser vi?! Vi har funnet det gyldne snitt! Du kan finne oppgaven løst i wxMaxima her.
Denne måten å generalisere oppgaven på er noe vi selvsagt ikke kan forvente at elevene skal klare på eksamen. Men med litt veiledning, så tror jeg noen av de flinkeste elevene kan klare det dersom de får tid og ro til å jobbe med problemet.
Hva er vi så ute etter på med denne oppgaven? Når har eleven gitt et fullgodt svar på spørsmålet om å kommentere resultatet (at vi får det samme forholdet i begge to tilfellene)?
Det første som slår meg er at elevene bør vise nysgjerrighet. Det å kunne stille spørsmål i matematikk er en del av den matematiske kompetansen. Men jeg forventer også at eleven viser en viss tilbakeholdenhet med konklusjonen. Ingen ting er bevist før det er virkelig bevist!
Siden denne oppgaven med fordel kan løses med et digitalt verktøy (som det står i oppgaveteksten) så jo eleven eksperimentert litt med flere ulike fjerdegradsfunksjoner. Dette kan gjøres i GeoGebra, som vist under. Her kan du endre på koeffisientene a, b, c, d og e og se hva som skjer med forholdet ST/TQ.
En anne kommentar: det står i oppgaven at eleven skal finne de ulike objektene (vendeunkt, tangenter, skjæringspunkt). En elev som styrer bra med GeoGebra løser denne oppgaven på noen få minutter, dersom vi godtar at alt gjøres på pc. Nedenfor ser dere hvordan jeg løste oppgave a) - d) (oppgave e er lik, bare med en ny funksjon -- lett å endre!)
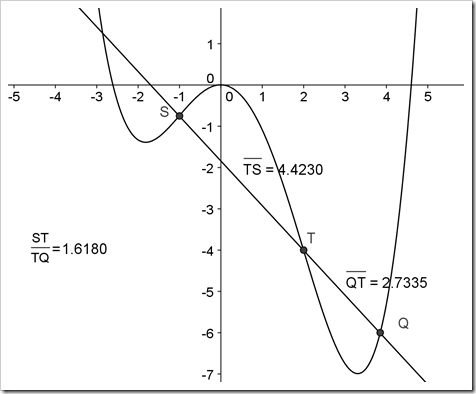


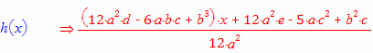


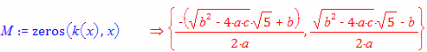



Det ble et fint resultat, jeg prøvde det samme i Maxima og fikk noe mindre lesbart.
SvarSlettHei! Hadde eksamen i R1 i går, og valgte selvfølgelig alternativ I på oppgave 4!
SvarSlettSer at du hadde et løsningsforslag til R1 i 2008, så jeg lurer på:
Lager du til denne også? :)
@Anonym Kanskje. Det kommer an på hvor fint vær det er ;-)
SvarSlettHadde blitt kjempetaknemlig om du hadde gjort det!
SvarSlettEr så spent på om jeg har fått til alt skjønner du, har en god følelse^^
Forresten, vet du noen plass jeg kan få tilgang på oppgavesettet som var gitt?
SvarSlett@Erik Espedal Boge: Du finner min løsning på Maxima her:
SvarSletthttp://tinyurl.com/rx7xao
Jeg valgte å dele vekk de to lineære faktorene svarende til vendepunktene selv om Maxima takler fjerdegradslikningen. Dette fordi jeg da lettere får tak på hva som er de to andre røttene...
Som du ser, så fikk også jeg en litt annen representasjon av det gyldne snitt. Men poenget er klart: det søkte forhold er uavhengig av a, b, ..., e.
Nå her jeg funnet ut hvordan maxima kan ordne rot-uttrykket. Du må laste inn en pakke som heter sqdnst (load(sqdnst)$) Da fikk jeg sannelig den ønskede representasjonen av det gyldne snitt. Se
SvarSletthttp://tinyurl.com/rx7xao
Svein Haugerudbråten og Christoph Kirfel har forøvrig skrevet en artikkel i Tangenten om denne egenskapen:
SvarSlettFjerdegradsfunksjoner og det gyldne snitt
Artig pakke, men Maxima har et stykke å gå siden det er enormt mange funkjoner som forenkler begrep, og ulike permutasjoner kan gi ulikt resultat. For noen er det godt med detaljstyring, men elevene mine hadde trengt en funksjon a la iPhotos tryllestav, som prøver alt den kan for å forbedre.
SvarSlettNøstede røtter er gjerne ikke det elever på vgs møter oftest, men nå når symbolbehandlerne kommer for fullt kan (må) uttrykkene gjøres mye vanskeligere enn det som er oppnåelig med blyant og formelsamling.