Hvor mye skal vi kreve av Fysikk 1- elever

Har nettopp hatt en prøve med mine Fysikk1-elever der en av oppgavene var som følger:

Ei kule henger i ein tynn snor i taket på ei stilleståande jernbanevogn.
Kva skjer med kula når toget setter seg i rørsle, og kvifor?

Nå sitter jeg og vurderer elevenes besvarelser og er litt usikker på hvor mye jeg kan forvente av dem. Her er hva en elev skriver:

Kula vil henge skrått bakover. Dette skjer fordi kula har treigleik.

Dette er jo i og for seg rett, men kan vi kreve en mer presis forklaring av elevene. Her er en annen variant:

Her blir Newtons 2. lov brukt. Hva sier du som leser denne bloggen?

Sektordiagram i GeoGebra

Det fins ikke eget verktøy for å lage sektordiagram i GeoGebra, men det går an å lage et slikt selv. Her i dette innlegget vil jeg ta deg med på prosessen som leder fram mot et slikt verktøy.

 

Vi starter med å åpne GeoGebra og lager en liste L med tall. Denne vil kun fungere som en dummy-liste. Skriv inn for eksempel L={4,3,4,1} i inntastingsfeltet:

Vi ønsker å finne de tilsvarende relative veridiene. Da må vi finne summen av listen, og så dele hvert element i listen med summen. For å finne summen av en liste skriver du inn:

 s=Sum[L].

Vi trenger også å vite hvor mange elementer listen har. I dette tilfellet ser vi at det er 4, men vi vil at dette skal fungere uavhengig av hvor mange elementer det er i listen L. Skriv derfor inn

a=Lengde[L].

Nå har vi det vi trenger for å lage en ny liste med de relative verdiene. For å gjøre dette bruker vi kommandoen Følge[ ]. Skriv inn

R=Følge[Element[L, i]/s, i, 1, a].

Her har jeg også brukt kommandoen Element[L, i]. Denne gir element nummer i i listen L. Kommandoen Følge alger en ny liste bestående av Uttrykk, Variabel, fra, til. Her i dette tilfellet er variabelen i og denne skal variere fra 1 til a. Alstå plukker vi ut elementene fra listen L og deler på summen s. Vi får da en ny liste med a elementer.

Så langt har vi altså fått følgende:

Vi vil nå lage enda en liste. Denne skal bestå av de tilsvarende vinklene som hvert element tilsvarer i et sektordiagram. Dette er ikke så veldig vanskelig siden vi nå har de relative verdiene. Vi må bare multiplisere hvert element i liste R med 360 grader. Vi skriver derfor inn

V=Følge[Element[R, i]*360°, i, 1, a]

Vi får da V={120°, 90°, 120°, 30°}. Men dette hjelper oss ikke helt, siden vi vil ha vinklene til hver sektor. Den første går fra 0° til 120° mens den andre skal går fra 120° til 120°+90°=210°. Vi må med andre ord lage en kummulativ liste med vinkler. Jeg skriver derfor inn:

W=Følge[Sum[V, i], i, 1, a]

Fa får vi W={120°, 210°, 330°, 360°}.

OK så langt. Vi har fått vinkelen. Neste steg er å finne selve punkta på sirkelen. Men først kan vi lage oss sirkelen. Lag et punkt en eller annen plass i Geometrivinduet. For eksempel

A=(3,3)

Velg en radius. For elsempel

r=2

Skriv så inn

Sirkel[A,r]

for å lage sirkelen med sentrum i A og radius r. Vi er nå klar for å lage punktene som derfinerer de ulike sektorene. Skriver inn:

P=Følge[A+r*(cos(Element[W,i]), sin(Element[W, i])), i, 1, a]

Du får da følgende figur:

Det neste jeg ønsker å gjøre, er å lege linjestykker fra A og ut til disse punkta. Skriver derfor inn:

M=Følge[Linjestykke[A, Element[P,i]],i,1,a]

En siste ting jeg ønsker å gjøre før jeg er klar til å lage verktøyet: jeg vil ta vekk navnet på sirkelen c. Høyreklikk på sirkelen og hakk vekk «Vis navn»:

 

Alt vel så langt. Vi er nå klare til å lage selve verktøyet. Klikk på Verktøy og «Lag nytt verktøy»:

Du vil da få opp vinduet som vist under. Her må du velge hvilke objekter du vil at verktøyet skal produsere. I vårt tilfelle er det linjestykkene og sirkelen:

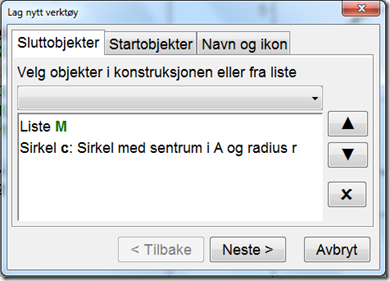
Disse skal lages ut fra listen L, punktet A og radiusen til sirkelen:

Velger du nå neste vil du få neste flik hvor du setter navn på verktøyet og hjelpetekst som forklarer hvordan verktøyet brukes. I dette eksempelet har jeg skrevet inn «Velg liste, sentrum av sektordiagram og radius»:

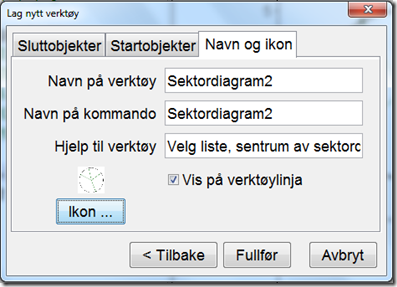
Klikk så fullfør og verktøyet er laget!

 

I bruk

La oss nå vise hvordan dette verktøyet kan brukes. Lag en ny liste med talldata:

H={13,10,20,5,4}

Helt til høyre på verktøylinjen har du nå fått et nytt verktøy (som vi akkurat har laget):

Jeg har flottet meg litt med å lage et ikon til verkøyet. Men dette er ikke nødvendig. Klikk på dette verktøyet og så på listen H. Deretter klikker du der du vil at sektordiagrammet skal være. Du vil da få følgende:

Skriv så inn ønsket radius til sektordiagrammet og du får det tegnet inn:

Dersom du synes dette var et verktøy som det er verdt å ta vare på, så bør du lagre innstillingene dine:

Da vil verktøyet være tilgjengelig hver gang du åpner GeoGebra!

Her kan du laste ned mitt verktøy.

 

En liten kommentar til slutt: egentlig er jeg ikke så begeistret for denne måten å tegne sektordiagram på. Vi får egentlig liten oversikt over tallmaterialet og verkøyet viser ikke hvilke tall hver sektor tilsvarer, selv om jeg vet at første sektor er første tall, andre er andre tall etc. Er det ikke bedre å bruke Excel til dette? Eller eventuelt OpenOffice.org Calc? Jeg synes at slike programmer er undervurdert i videregående skole!

En artig liten sak…

Elstemann har blitt 13 år og dermed er jeg ikke lenger den enerste i huset som er registrert på Facebook. Her om dagen la han ut følgende på statusen sin:

Hvem er ditt idol?
Du må ikke jukse...
1: Tenk på et tall mellom 1 og 9.
2: Multipliser tallet med 3.
3: Legg til 3.
4: Multipliser tallet med 3
Du får nå et tosifret tall.
5: Legg sammen de to sifrene
Nå kan du ser med ditt tall hvem som er ditt idol:
1. Kesha
2. Barrak Obama
3. Michael Jackson
4. Taio Cruz
5. Madcon
6. Raske menn
7. Lady Gaga
8. Katy Perry
9. Mathias Kristensen
10. Ozzy Osbourne

Så her har du en liten utfordring: hvordan eller hvorfor fungerer dette?

Bilder til presentasjoner…

Når jeg lager presentasjoner, så liker jeg å bruke bilder dersom det er tjenelig. Jeg ser at mange henter bildene fra google og det er i og for seg greit. Men vi har jo det juridiske aspektet her. Hva har vi lov til å bruke? I dette lille blogginnlegget vil jeg bare tipse om en veldig bra tjeneste levert av Microsoft. Gå til http://office.microsoft.com/nb-no/ og velg bilder i menyen under søkefeltet:

 

Søker du for eksempel etter bilder med søkeordet «geometri», så får du følgende svar:

La oss si at jeg liker bildet bederst til venstre. Holer du markøren over dette bildet, vil du få følgende vindu opp:

Klikk så på «Vis lignende bilder». Du vil da få flere biler i samme stil:

  

På den måten kan du finne mange gode bilder tatt av profesjonelle fotografer. Du laster ned et bilde ved å høyreklikke en gang på det, vente litt og velge «Last ned»:

Dette krever at du har installert Silverlight. Men det får du fort nok beskjed om, dersom du mangler dette… 

Anki – for å lære noe utenatt…

I dag kom jeg over et bra lite program som er laget for å hjelpe oss å memorere ulike fakta. Programmet heter Anki og kan lastes ned fra http://ichi2.net/anki/ . Selve programmet er bygget opp slik at du laster ned «kort» fra et tema. Det kan være norske uregelmessige verb, fysiske konstanter, eller ulike fakta innenfor geometri.

 

Du laster ned nye kortstokker ved å klikke på last ned:

 

 

Du vil da få opp en lang liste med ferdige kortstokker. Du kan selvsagt også lage egne kortstokker om du ønsker det.

 

 

Jeg har lastet ned Euclidian and Non-Euclidian Geomatry. Selve opplegget funker slik. Du får opp et kort med et psørsmål:

Så skal du si til deg selv hva svaret er før du klikker på «Vis svar»:

Du velger så om du synes dette var veldig lett,lett, bra eller om du trenger dette repetert om ikke veldig lenge.

 

Hva kan vi så lære av denne typen program? Vi lærer visse fakta. That’s it. Men fakta er ok å kunne, så det kan være artig å prøve dette programmet…

Zoomìng på skjermen

Jeg holder en del kurs i digitale verktøy, og i den forbindelse er det min erfaring at det alltid er deltakere som har problemer med å se hva som står på lerrete når jeg skal vise for eksempel ulike menyer. Det er stor forskjell på dette:

og dette:

Dette er selvsagt ikke vanskelig å få til når du jobber med bilder av skjermen (slik jeg gjør i dette innlegget. Men hva om du ønsker noe slik:

Her har jeg brukt et flott lite program som heter ZoomIt. Dette kan du laste ned her. I ZoomIt kan du lage egne snarveier. Det fins fire ting du kan gjøre med dette programmet: zoome, skrive og tegne på skjermen, og du kan sette på  nedtelling til pauseslutt:

 

Et annet kjekt program som kan brukes er Virtual Magnifying Glass. Det funker slik at du får et forstørrelsesglass når programmet aktuveres og dette er aktivt helt til du klikker neste gang. Litt enklere, men mangler funksjonalitet som gjør det mulig å se hva du driver på med samtidig som du zoomer (slik ZoomIt gjør).

 

Å undervise på studieforberedende…

Videregående skole er organisert i yrkesfaglige og studieforberedende utdanningsprogram. Jeg underviser for det meste på sistnevnte studieprogram og i dette innlegget vil jeg komme med noen tanker jeg har om å undervise elever på dette studieprogrammet. Selve innlegget er et forsøk på å svare på en utfordring jeg fikk i et tidligere innlegg der jeg skriver at det er viktig at vi ikke bare lærer elevene fagkunnskap men også å lære dem å studere.

 

Jeg har i løpet av min yrkeskarriere så langt undervist i grunnskole, videregående, høgskole og universitet. Som høgskolelektor slo det meg ofte at mange av studentene ikke var i stand til å lese en matematikkbok. Det er noe jeg synes er tristere enn at de for eksempel ikke mestrer brøkregning eller at de ikke klarer å tegne en graf ordentlig. For dersom de er i stand til å lese matematikk, så vil det være et mindre problem å lære noe nytt senere om det skulle bli nødvendig. Det samme gjelder dette med problemløsningskompetanse. Jeg synes det er mye viktigere at elevene blir gode problemløsere enn at de kan løse avanserte differensiallikninger. Det siste er egentlig ikke vanskelig, kun litt teknisk krevende. Men oppskriften har vi jo i boka, ikke sant?

 

Så hva innebærer det å lære elevene å studere matematikk? Hva er det vi vil? Her er noen ting jeg synes er viktig:

• Elevene skal kunne lese matematiske tekster på egen hånd
• De skal kunne forstå et matematisk problem og kunne prøve ulike strategier for å kunne løse det
• De skal kunne skrive matematikk. Det vil ikke si at de skal kunne bruke MathType, LaTeX eller hva det måtte være, men at de skal bli i stand til å formulere argumenter og bruke et presist språk
• De skal kunne vurdere egne og andres matematiske resonnement og få en spørrende og kritisk måte å tenke på. Det vil si at de skal kunne tenke matematisk.  Det vil si at de skal utvikle det Alan H. Schoenfeld kaller «a mathematical point of view».

Er det forresten ikke dette som står i formålet til faget? Jeg mener det! Men det store spørsmålet er: hvordan skal vi få dette til?

 

Vi har nettopp fått publisert en ny TIMSS-rapport. Og vi blir igjen skuffet. Det går ikke særlig bra med norske elever når vi ser på deres matematikklæring. Denne gang var det avgangselever i videregående som var under lupen. Riktignok ikke elever under kunnskapsløftet, men jeg tror ærlig talt ikke at det spiller noen rolle. Mitt poeng er at TIMSS advanced avslører noe jeg lenge har fryktet: elevene jobber alt for mye individuelt med oppgaver som ligner på eksempler i læreboka. Følgende figur viser dette (tatt fra TIMSS-rapporten):

Legg også merke til at det blir lite diskusjoner av resonnementer og løsningsstrategier blant elevene i Norge og at de jobber lite med sammensatte problemer.

 

Dette er noe jeg strever med. Når vi innfører et nytt emne med elevene, så føler jeg at temaet må få modnes hos elevene og at de i denne fasen må få jobbe med det som Aschehoug sitt læreverk kaller for innlæringsoppgaver. Men da melder problemet seg: får de da tid til å jobbe med mer sammensatte oppgaver og problemløsningsoppgaver? Pensumet i R2 er gangske stort og jeg sliter litt med dette. Men kanskje det er mulig å lære seg nytt stoff via problemløsningsoppgaver? Dette er noe jeg mener vi ikke har kultur for i Norge. Og da mener jeg at både lærer og elever ikke er vant med dette og at det kan være problematisk med en slik tilnærming til stoffet. Men uansett: det er der jeg ønsker å komme og jeg mener at dette er mulig. TIMSS video studies har dokumentert at dette er noe de får til i Japan, så da er det kanskje mulig også i Norge?

 

Så her er noen prinsipper jeg ønsker å følge i min undervisning:

 

• Elevene skal ikke bare jobbe med innlæringsoppgaver, men også problemløsningsoppgaver
• Elevene skal ikke bare jobbe individuelt, men jeg må passe på å skape situasjoner der ulike ideer og strategier blir diskutert
• Det skal være lov å feile i mine timer.
• Elevene skal ikke få servert alt fra meg. Jeg må passe på at de også selv må sette seg inn i ulike tema. Dette kan innebære at de må få utfordringer som krever at de selv må sette seg inn i nytt stoff.
• Eleven må utfordres til å kommunisere sine ideer. Når vi har hatt en prøve, så vil jeg diskutere ulike måter å svare på og på den måten få fram gode eksempler som elevene kan lære fra.
• Jeg må lære elevene til å overvåke sin egen læringsvirksomhet. Dette innebærer at de lærer å stille seg selv kritisk spørsmål. Hvorfor gjør jeg dette? Er dette lurt? Hva er det vi vet? Har jeg sett noe liknende før? Hvorfor må vi anta at dette eller dette gjelder? Hva om dette gjelder?

Jeg kan ikke skryte over at dette er noe jeg får til. Men jeg kan si at dette er noe jeg jobber mot. Dette er min visjon for undervisningen. Av og til lykkes jeg, ofte gjør jeg det ikke. Men noe må vi ha å jobbe mot, ikke sant?

GeoGebra tips & triks

Etter å ha holdt en del kur for lærere (og elever) i GeoGebra, så ser jeg at en del kan ha glede av en samling av tips og triks som jeg bruker i GeoGebra. Så hva er vel en bedre plass å dele disse enn her på bloggen? Har du andre nyttige tips, så del dem gjerne!

 

Tips 1: Hurtigtaster

Det fins mang slike hurtigtaster, og jeg vil ikke komme med noen utfyllende liste her. Det er det vel ingen som vil huske uansett? Så her er de jeg bruker mest:

Taster	Beskrielse
Ctrl+n	Åpne ny GeoGebrafil i nytt vindu
Ctrl+s	Lagre
Ctrl+Shift+S	Åpne regnearkvinduet
Ctrl+Shift+C	Kopiere geometrifeltet til utklipstavlen slik at du kan lime det inn som bilde i for eksempel en Word-fil (Ctrl+v)
Alt+2	2 (opphøyd i 2)
Alt+3	3 (opphøyd i 3)
Alt+9	9 (dvs at dette fungerer for alle tallene fra 2 til 9.)
Alt+p	π
Alt+e	e (Eulers tall ≈2,7182818284590)
Alt+o	«Grader»
Alt+Shift+;	≤
Alt+Shift+:	≥
Alt++	±
Alt+a	α (flere andre bokstaver gir sammen med «Alt» en gresk bokstav:
Alt+s	σ

 

Tips 2:

Dersom du skal skrive inn en kommando i inntastingsfeltet er det bare å trykke enter og du kan begynne å skrive inn kommandoen.

Tips 3:

For å fullføre en kommando i inntastingsfeltet er det bare å tykke på enter:

Tips 4

Du kan bla i tidligere kommandoer som du har skrevet i inntastingsfeltet ved å bruke piltastene (opp for tilbake i tid).

Tips 5

Om du ikke husker en kommando, så finner du de aller fleste under menyen Kommando… nederst til høyre:

Tips 6

Du kan endre skriftstørrelsen til menyer etc i GeoGbra under innstillinger (1). Velg passe fontstørrelse (2) og lagre innstillinger (3) for at endringene skal gjelde neste gang du åpner GeoGebra.

 

Tips 7

Du kan angre noe du har gjort i GeoGebra ved å trykke Ctrl+z eller klikke på knappene øverst til høyre i GeoGebra.

Tips 8

Du kan zoome inn og ut ved å skrolle dersom du har mus med skrollehjul. Du kan også skalere en akse ved å holde Ctrl-knappene nede og så dra i aksene. Pass på at markøren ligger over aksen og at den har blitt til en pil.

Tips 9

Dette er kanskje det beste tipset (?). Dersom du skal bruke en kommando, men husker ikke hva du skal skrive, så gir du bare kommandoen uten noen argumenter og trykker enter. Du vil da få opp en feilmelding. I denne får du se hvordan syntaksen for kommandoen er:

Tips 10

Dersom du virkelig står fast eller det er noe du skulle ha fått til, men vet ikke helt hvordan det gjøres, så trykk F1 og du vil få opp (i nettleseren din) brukermanualen til GeoGebra. Her står det meste. Dersom dette ikke hjelper deg, så er det flere forum hvord du kan henvende deg. Det er nok av frivillige som vil svare! Her er noe steder du kan prøve:

• http://www.geogebra.org/forum/ (her er også et eget forum på norsk)
• http://delogbruk.ning.com/group/geogebra Dette er GeoGebra-gruppen på Del & Bruk.