Minste kvadraters metode i R2

For tiden jobber vi med modellering i R2. I den forbindelse skal elevene kunne utføre ulike typer regresjoner. Den vanligste av disse er lineær regresjon: gitt en del punkter i planet. Finn så den linjen som passer best (i en eller annen forstand) til disse punktene.

Jeg har alltid hatt en følelse av at dette blir veldig mekanisk og kunstig for elevene. Trykk på noen knapper på kalkulatoren eller pc-en og vips så får du linjen. Men hva er det egentlig som skjer? Hvilken matematikk ligger bak denne formelen? Dette er noe som blir lite lagt vekt på i lærebøkene. Det synes jeg er litt dumt. Da tror jeg faktisk at elevene ville være bedre tjent med å kutte ut hele regresjonsgreie og heller jobbe med forståelse innenfor andre tema. Men det er nå bare min mening.

 

Så hvordan kan vi så gjøre dette mer forståelig for elevene? Jeg vil ikke komme med noe fasitsvar på dette her, men vil skissere en måte å gå fram på. Hvor mye elevene faktisk sitter igjen med etter en slik gjennomgang er ikke godt å vite og avhenger selvsagt av bakgrunn og motivasjon til eleven.

 

Det går an å gjøre en innføring som appelerer til intuisjonen til elevene. Jeg har laget et lite GeoGebra-arbeidsark som kan brukes i denne sammenhengen. Selve ideen til arket har jeg fra GeoGebra-wikien, men må dessverre si at jeg ikke har klart å finne originalen igjen. Så her er min versjon.

 

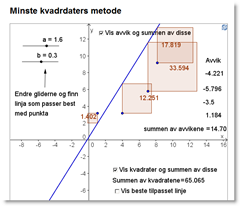
Som du kan se, så har jeg lagt inn fire punkt i arket og en linje y=ax+b. Opplegget går så ut på å fikle med gliderne til vi får en linje som «passer bra». Legg merke til at du kan få summen av avvikene til å være konstant innenfor visse intervall av glideren b. Dette viser at selve avvika ikke er egnet som mål for hvor godt linja passer. Dette må selvsagt diskuteres med elevene i fellesskap. Noen elever vil så foreslå at vi kan bruke absoluttverdien av avvikene og det er selvsagt helt korrekt. Men det er ikke så lett regneteknisk. Derfor fant Gauss ut at summen av kvadratavvikene vil være et bedre mål. Ved å klikke på avkrysningsboksen for «Vis kvadrater og summen av disse» vil du få fram kvadratene. Poenget nå er å finne den a og b som gjør denne summen minst mulig.

 

Forhåpentligvis har de fleste elevene fått med seg ideen nå. Skal vi så stoppe der, eller bør vi dra dem et steg videre? Her er jeg litt usikker, men i år valgte jeg det siste. Jeg tok utgangspunkt i et eksempel. La oss si at vi vil finne linja som passer best til punkta (1, 2), (4, 5) og (7, 7). Vi ønsker med andre ord å finne en funksjon f(x)=ax+b som er slik at summen av kvadratene til avvikene blir minst mulig. Avvikene blir i dette tilfellet f(1)-2, f(4)-5 og f(7)-7. Det vil si at summen av kvadratene til disse blir:

Det er denne summen vi ønsker å gjøre så liten som mulig. Dersom vi nå bare ser på b som en konstant og a som vår variabel, så kan vi derivere med hensyn på a. Dette kalles partiellderivasjon og fungerer på samme måte som vanlig derivasjon. Vi noterer dette som   Vi vet at dersom det er en a (og en b) som gjør denne summen minst mulig, så må den deriverte med hensyn på a være null. Vi får:

På samme måte må den deriverte med hensyn på b være null:

Vi har med andre ord fått to likninger med to ukjente a og b. Løser vi dette likningssettet, så får vi a=5/6 og b=4/3. Altså har den linjen som gir minst minste kvadratsum gitt ved

 

I videregående tror jeg det neppe er noen god ide å dra dette videre og vise det generelt. Men de aller aller flinkeste kan kanskje klare å finne ut av den generelle formelen for a og b selv. Men det gjør jeg ikke her i bloggen .

 

Prosedyrene beskrevet over er selvsagt ikke noe vi skal gjøre hver gang vi skal gjøre regresjoner. Så i det videre arbeidet vil elevene mine bruke GeoGebra.

 

Et lite tips til slutt. Det fins mange kommandoer for regresjon i GeoGebra. To av disse er RegLin og RegPloly. Sistnevnte kommando tar to argumenter: liste med punkter og grad. Velg grad lik 1. Dette er bedre enn RegLin siden denne kun gir en linje som var, mens RegPoly gir en funksjon som svar. Dette er mye bedre dersom vi i en modell skal finne hva y er når x er gitt. Da er det bare til å regne ut f(x)!

 

Helt til slutt: synes du det er å presse elevene for mye når jeg tar dem med på slike partiellderiveringer, eller tror du dette kan være med på å øke den matematiske forståelsen til elevene? Jeg spør fordi jeg er usikker!