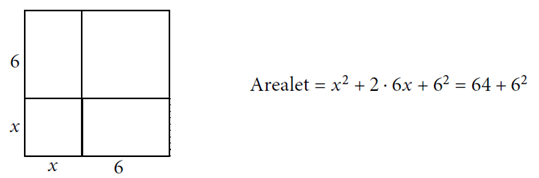I Matematikk 1T skal elevene lære å løse andregradslikninger. Det vil si at de skal kunne løse likninger på formen I Aschehaougs læreverk blir elevene presentert løsningsformelen for denne – den såkalte abc-formelen:
Dette blir gjort uten bevis eller noe argumentasjon. I Cappelen Damm sitt læreverk Sinus blir formelen presentert og det blir gitt noen eksempler og oppgaver før beviset blir gitt.
Jeg liker dårligst Aschehougs versjon. Formelen blir presentert og jobbet med i kapittel 1 og det er først i kapittel 5 at elevene blir introdusert til kvadratsetningene. Dette synes jeg er meget uheldig. Elever som velger 1T må for all del ikke lære at matematikk er et fag der de skal lære et sett med regler og prosedyrer som de skal kunne. Matematikk er mer enn dette. Eller kanskje vi kan si at dette ikke er matematikk i det hele tatt?
Jeg vil i dette innlegget dele noen tanker om hvordan jeg liker å introdusere elevene til kvadratiske likninger. Jeg pleier å starte med helt enkle likninger av typen . Geometrisk kan vi si at dette svarer til lengden av sidene i et kvadrat med areal lik 9. Men vi må selvsagt ikke glemme den negative løsningen. Når elevene har fått diskutert dette kan vi se på likninger av typen
. Det vil si at
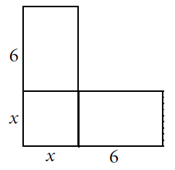
Dette pleier å gå greit. Problemet oppstår når vi skal se på likninger av typen . Nå er det ikke bare til å flytte over og ta kvadratrot. Her må det jobbes mer og det kan være instruktivt å gi en geometrisk løsning også her. Målet er jo at elevene skal forstå konseptet med å fullføre kvadrater. I dette tilfellet svarer likningen til å finne x slik at arealet til følgende rektangel blir lik 64:
Trikset vi her gjør er å dele biten til høyre i to like store deler:
Klipper vi opp langs den oransje linjen og flytter på den ene rektanglet, får vi:
Dette begynner å likne på et kvadrat. Den delen sommangler for at dette skal
bli et kvadrat har et areal som er . Det vil si at figuren under er 36
arealenheter større enn den opprinnelige figuren:
Denne figuren har med andre ord et areal lik 64 + 36 = 100. Sidene i dette
kvadratet har lengder lik x + 6. Vi får derfor:
Vi kan nå ta kvadratroten av begge sider og få
Det vil si at x=4 eller x=-16.
Når dette er gjort pleier jeg å gi tilsvarende oppgaver og kanskje noen med en liten vri på. Jeg har laget et lite hefte som viser mer detaler.
Poenget er at elevene forhåpentligvis vil forstå hva det innebærer å fullføre et kvadrat og at kanskje noen vil forstå den generelle utledningen av acb-formelen.
Synes du dette var interessant, kan du selvsagt bruke heftet lenket ovenfor.