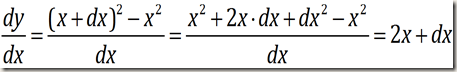I forbindelse med noen kjennetegn på måloppnåelse som jeg har laget til R1 (og S2), ble det en interessant diskusjon av hva vi kan forvente oss av en elev som velger matematikk R1. Utgangspunktet var kompetansemålet som tar for seg grenser og kontinuitet. I LK06 står det at eleven skal kunne gjøre rede for begrepene grenseverdi, kontinuitet og deriverbarhet, og gi eksempler på funksjoner som ikke er kontinuerlige eller deriverbare. Hva betyr dette? Hvor presist skal vi kunne forvente oss at eleven skal kunne gjøre rede for grensebegrepet? Hva kjennetegner høy grad av måloppnåelse?
For å svare på dette, vil jeg ta et lite historisk tilbakeblikk. Deretter vil jeg se litt på læringsteoretisk modeller som sier noe om abstraksjonsnivået og forståelse av matematiske begreper.
Historiske betraktninger
De første antydningene til et grensebegrep finner vi allerede i antikkens verden. Eudoksos fra Knidos er kjent for uttømmingsmetoden (engelsk: method of exhaustion). Denne videreutviklet Euklid, og essensen er at du kan f.eks. finne arealet av en sirkel ved å innskrive et regulært polygon. Dersom du øker antall kanter, så vil arealet til polygonet stadig bli mer lik arealet til sirkelen. Dersom du lar antall kanter gå mot uendelig, så vil du få likhet. Men dette ville selvsagt ikke grekerne gjøre, som ungikk uendelighetsbegrepet for enhver pris. Men prinsippet var der: Du kan få arealet til å bli bedre og bedre, dess flere kanter polygonet har.
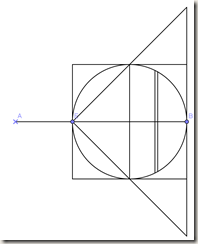 Arkimedes brukte denne metoden til å finne volumet av en kule med en gitt radius. Her var ideen å dele opp visse figurer i små skiver med en liten tykkelse (i dag ville vi klalt tykkelsen ∆x). Ved å ballansere disse skivene på en vektstang og bruke at angulært moment er null (hopper over detaljer her, kommer tilbake til dette ved et senere innlegg), så fant han til slutt ut at volumet av en kule er fire ganger arealet til en sirkel med samme radius delt på tre. I resonnementet her må vi la ∆x gå mot null. Og det var det Arkimedes i praksis gjorde. I dag vil vi si at Arkimedes regnet ut et integral. Men slike begreper snakket de ikke om på den tid.
Arkimedes brukte denne metoden til å finne volumet av en kule med en gitt radius. Her var ideen å dele opp visse figurer i små skiver med en liten tykkelse (i dag ville vi klalt tykkelsen ∆x). Ved å ballansere disse skivene på en vektstang og bruke at angulært moment er null (hopper over detaljer her, kommer tilbake til dette ved et senere innlegg), så fant han til slutt ut at volumet av en kule er fire ganger arealet til en sirkel med samme radius delt på tre. I resonnementet her må vi la ∆x gå mot null. Og det var det Arkimedes i praksis gjorde. I dag vil vi si at Arkimedes regnet ut et integral. Men slike begreper snakket de ikke om på den tid.
Hopper vi fram ca 1900 år kommer vil til Newton og Leibniz. Disse blir regnet som grunnlegerne av integral- og differensialregningen. Ideene bak Newtons og Leiniz’ teori er nok så like, men notasjonen er ganske annerledes. Det er fra Leibiz av vi har skrivemåten dy/dx. Han regnet uhemmet med infinitessimaler. Det vil si uendelig små størrelser. Dersom vi skal derivere funksjonen y=x2 så ser vi på kvotienten
Setter vi nå dx=0, så får vi at den deriverte til y=x2 er lik 2x, dvs at dy/dx=2x. Men kan vi egentlig gjøre dette? I kvotienten vi startet med delte vi jo på dx, og så satte vi plutselig dx=0… Dette kan vel ikke være lov?
 Newton derimot snakket om sine “fluents”. Det vil si at han så på de variable som størrelser som kunne endre, akkurat som en flytende strøm av veske kan endres. Newton ville sagt at dx skulle flyte mot null (selv om han ikke akkurat brukte denne notasjonen. Newton ville ha byttet ut en variabel z med z+oż og latt o forsvinne mot null).
Newton derimot snakket om sine “fluents”. Det vil si at han så på de variable som størrelser som kunne endre, akkurat som en flytende strøm av veske kan endres. Newton ville sagt at dx skulle flyte mot null (selv om han ikke akkurat brukte denne notasjonen. Newton ville ha byttet ut en variabel z med z+oż og latt o forsvinne mot null).
Den første kritikeren til denne måten å resonnere på kom utenfra. Det var biskop George Berkeley (1685 – 1753) som satte fingeren på problemet i artikkelen The analyst. Der skriver han kritisk om Newtons “fluxions” (disse o-ene som går mot null):
And what are these fluxions? The velocities of evanescent increments. And what are these same evanescent increments? They are neither finite quantities, nor quantities infinitely small, nor yet nothing. May we not call them ghosts of departed quantities?
Det var ikke vanskelig å se at Berkeley hadde et poeng. Noe måtte gjøres og kanskje den første som tok et tak i dette var Jean-le-Rond d’Alembert (1717-1783). Han forslo at integral- og differensialregningen skulle bassere seg på grenser. Ideen hans var å se på kvotienenten u/z=(f(x+∆x)-f(x))/∆x (i vår notasjon). Han definerte da dy/dx til å være det tall som u/z nærmet seg når u og z nærmet seg null. Vi ser her at grensebegrepet begynner å komme tydeligere fram. Men det er fremdeles upresist etter dagens standard. Men d’Alembert var på rett spor.
 Neste store matematiker som jeg vil trekker fram er Cauchy. Han formulerte en enda mer presis formulering av grensebegrepet:
Neste store matematiker som jeg vil trekker fram er Cauchy. Han formulerte en enda mer presis formulering av grensebegrepet:
When the values successively attributed to the same variable approach a fixed value indefinitely, in such a way as to end up by differing from it as little as one could wish, this last value is called the limit of all the others.
Legg merke til at Cauchy bruker ord som approach. Det vil si at det fremdeles er en slags dynamisk forståelse av grensene. Det er noe som nærmer seg noe annet. Det var først Weierstass som laget en statisk deinisjon – den så kalte epsilon-delta-definisjonen. Den lyder slik:
Vi sier at f(x) får mot L når x går mot a dersom det er slik at for enhver ε>0 finnes en δ>0 slika at 0<| x-a |< δ medfører at | f(x) - L |<ε.
Didaktiske betraktninger
I den lille historiske gjennomgangen over håper jeg å ha fått fram tydelig at grensebegrepet har en lang historie og at det tok lang tid før vi fikk den presise definisjonen som vi bruker i dag. Mitt poeng er at vi ikke gjør noe feil når vi ikke tar med den rigoriøse Weierstrass-definisjonen, vi er bare ikke så presise. Jeg tror at Newton hadde en viss forståelse for grensebegrepet, for å si det på den måten. Men det betyr nødvendigvis ikke at vi ikke skal kunne forvente at flinke elever skal kunne klare å jobbe med en slik definisjon. Eller?
Jeg synes det er viktig at elever i videregående skole som har ambisjoner innenfor realfaga ikke bare får øvelser i å regne, men at de også får en viss forståelse for den formelle siden med faget. Viser en elev som kan regne ut grenser ved å faktorisere visse polynomer, forkorte og så sette inn grenseverdien at han eller hun har høy måloppnåelse (karakter 5 eller 6)? Ikke sånn i utgangspunktet! Hva skal så til? Min konklusjon så langt er at en dynamisk forståelse er bra nok på dette nivå. Jeg forventer at eleven skal si at funksjonen nærmer seg en viss verdi når x nærmer seg en verdi, men ikke bli lik. Det vil si at jeg ikke krever mer enn det som d’Alembert sa. Det betyr ikke at en elev ikke skal møte epsilon-delta-definisjonen, men at dette vil være mer en hva som skal til for å få topp karakter.
En annen ting. Kan vi forvente at den jevne elev skal få utbytte av en slik rigoriøsitet? Det tviler jeg litt på. Det er en del pedagogiske teorie som prøver å beskrive elevers læring. Mange av disse går i retning av ulike taxonomier. Det vil si at elevene ikke har en kontinuerlig læringskurve, men at det går litt i rykk og napp. Den mest kjente teorien er kanskje Piagets stadieteori. En annen slik taksonomi er den så kalte SOLO-taksonomien til Biggs og Collis. SOLO står for
Structure of
Observed
Learning
Outcomes
I denne er det fem nivå:
- Pre-strukturelt: eleven skaffer seg usammenhengende informasjon.
- Uni-strukturelt: enkle og opplagte sammenhenger finnes, men blir ikke brukt på en vesentlig måte
- Multistrukturelt:En rekke sammenhenger blir brukt, men ikke på en helhetlig måte.
- Relasjonelt: Eleven klarer å se ulike sammenhenger i relasjon til hverandre.
- Utvidet abstrakt: eleven ser ikke bare sammenhenger ut fra en kontekst, men klarer å generalisere disse til andre områder.
Felles for slike taksonomier er at i det øverste nivået viser elevene evne til abstraksjon og teoretisering. van Hieles har også en slik taksonimi knyttet til geometriske former. På det øverste nivå i van Hieles har vi aksiomatisering. Mitt poeng er at en statisk forståelse av grenseberepet forutsetter at eleven er på et utvidet abstrakt nivå, noe jeg tviler mange elever på vg 2 er. Men dette har jeg egentlig ikke dekning for å si. Det er kun bassert på erfaringer.
Konklusjonen min er derfor at det blir for mye å forvente av en elev på vg2 at han eller hun skal kunne aktivt bruke epsilon-delta-definisjon for å bevise ulike grenseverdier. Men noen elever er der, og disse kan godt møte slike utfordringer allerede i videregående skole. Men har vi tid til slilk tilpasset opplæring?