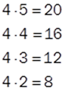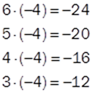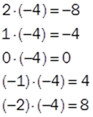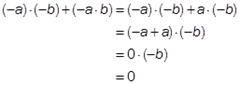Hva er matematikk? Det er et ganske dypt spørsmål og det fins et hav av svar på dette spørsmålet. På den ene siden kan faget bli sett på som en samling av fakta og ferdigheter. Å lære matematikk vil ut fra et slikt syn si å kunne mestre algoritmer, kunne gjengi teoremer og huske ulike definisjoner. På den andre siden kan vi si at matematikk er «vitenskapen om mønster» (engelsk: science of patterns). Ut fra dette synet går matematikk ut på å lete etter mønster og sammenhenger.
Heldigvis trenger vi ikke å velge ståsted. Matematikk er mer enn fakta og ferdigheter, men disse er også viktige deler av faget. Vi søker å finne sammenhenger og algoritmer. Når vi har funnet en sammenheng, så prøver vi å bevise denne ut fra visse formelle spilleregler. Når dette er gjort og vi således har klart å bevise resultatet sier vi at vi har et teorem.
Et kjent eksempel på dette er Fermats siste sats. Denne sier at det ikke finnes hele tall a, b og c slik at
![tex:[[a%5En%2Bb%5En%3Dc%5En]]](http://www.mathtran.org/cgi-bin/mathtran?tex=a%5En%2Bb%5En%3Dc%5En)
for heltall,
![tex:[[n%5Cgeq%203]]](http://www.mathtran.org/cgi-bin/mathtran?tex=n%5Cgeq%203)
. I tilfellet n=2 gjelder dette ikke, for der har vi alle de pytagoreiske triplene, for eksempel
![tex:[[3%5E2%2B4%5E2%3D5%5E2]]](http://www.mathtran.org/cgi-bin/mathtran?tex=3%5E2%2B4%5E2%3D5%5E2)
. Poenget her er at ingen klarte å bevise at denne satsen var sann før Andrew Wiles klarte det i 1995. Det var 358 etter at Pierre de Fermat satte fram sin formodning i margen til Diofantos bok
Aritmetica. Hvordan «visste» så Fermat og alle matematikere som i århundrene etter prøvde å finne et bevis at dette stemte? Det var små biter som alle pekte mot denne sammenhengen. Faktisk klarte Leonardi Fibonacci å bevise at «Fermats sats» stemte for n=4 allerede i 1225. Euler viste at satsen var rett for n=3 i 1770 og Sophie Germain klarte å vise den for alle primtall mindre enn 100. Men det var altså Andrew Wiles som endelig klarte å bevise resultatet generelt.
Det er alltid interessant å studere hvordan matematiske sammenhenger oppdages og bevises i et historisk perspektiv. Tar du en standard tekstbok i matematikk, så ser alt så rent og pent ut med en logisk oppbygging. Dette viser strukturen i faget. Dette er noe som alltid har fasinert meg og er trolig grunnen til at jeg valgte algebraisk geometri. I algebraen er selve strukturene essensen av det vi studerer. Vi konstruerer visse objekter og lager en additiv og multiplikativ struktur. De som har studert lineær algebra vil se dette tydelig i teorien om vektorrom.
Men hva har dette å si for undervisningen i videregående skole? Dessverre er det lite leting etter mønster og sammenhenger i lærebøkene. Selv om det er mange gode unntak for det jeg her skriver, så tror jeg ikke at jeg er langt fra sannheten når jeg sier at lærebøkene legger lite opp til at elevene skal utforske og oppdage sammenhenger. Og dessverre blir også den formelle siden neglisjert.
La meg ta et eksempel. Elevene får allerede i ungdomsskolen lære at når du ganger sammen to negative tall, så vil svare bli et positivt tall -- eller som det ofte heter: minus og minus er pluss. Men hvordan kan elevene «vite» at dette stemmer? Jeg har satt vite i anførselstegn siden det etter min mening fins flere nivåer i det å vite noe. Fermat var gangsk sikker å at satsen hans var sann. Han bare visste det. Men det var egentlig ingen som visste det før i 1995.
Her er en måte som jeg har hatt suksess med når det gjelder regelen «minus ganger minus er positiv». Start med to positive tall, la oss si 4 og 5. Spør så elevene hva du får når du ganger dem sammen. Svaret er 20. Reduser så systematisk det ene tallet slik at du får følgende liste med regnestykker:
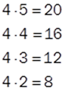
Hva er sammenhengen her? Er det noe mønster i svara? Her er tanken at elevene selv skal se at svaret reduseres med 4 nedover. Så da blir de to neste tall 4 og 0. Så hva blir da
![tex:[[4%5Ccdot%20%28-1%29]]](http://www.mathtran.org/cgi-bin/mathtran?tex=4%5Ccdot%20%28-1%29)
? Det er 4 mindre enn 0 ikke sant? Altså -4. Hva så med
![tex:[[4%5Ccdot%20%28-2%29]]](http://www.mathtran.org/cgi-bin/mathtran?tex=4%5Ccdot%20%28-2%29)
? Det blir -8. Sammenhengen er oppdaget: et positivt tall multiplisert med et negativt tall er det tilsvarende negative tallet.
Når denne sammenhengen er oppdaget fortsetter vi med å utforske hva som skjer om vi starter med et negativt og et positivt tall, for eksempel 6 og -4. Vi gjentar så oppsettet over og spør hva vi får når vi ganger sammen disse. Svaret blir -24 ikke sant? Så reduserer vi 6:
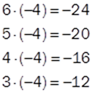
Hva er så sammenhengen her? Jo, når vi reduserer tallene til venstre, så øker svaret med 4 nedover. Så da blir de neste tallene -8, -4 og 0. Det store spørsmålet nå er hva
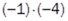
blir? Det er vel 4 mer enn 0 det da! Akkurat! Så da kan vi fortsette:
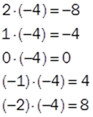
Hvilken sammenheng ser vi? At et negativt tall multiplisert med et negativt er et positivt tall!
Hva så med den formelle siden? Hvordan beviser vi en slik sammenheng? Når jeg nå skal gå igjennom et slikt bevis, så tror jeg mange vil forstå hvorfor dette ikke blir gjort for de fleste elevene. Men da jeg underviste på ungdomstrinnet tok jeg de flinkeste elevene til sides og viste dem beviset. Dette var for elever i 9. trinn og dersom du rynker på nesen over dette, så vil jeg si at det er min faste oppfatning at de flinkeste elevene kan presses mye lenger enn det vi ofte gjør. Men her er beviset. Vi starter med å se på
![tex:[[%20a%5Ccdot%20%28-b%29]]](http://www.mathtran.org/cgi-bin/mathtran?tex=%20a%5Ccdot%20%28-b%29)
. Vi ønsker å vise at dette blir
![tex:[[%20-%28a%5Ccdot%20b%29]]](http://www.mathtran.org/cgi-bin/mathtran?tex=%20-%28a%5Ccdot%20b%29)
. En fin måte å gjøre dette på er å vise at når du adderer
![tex:[[%20a%5Ccdot%20%28-b]]](http://www.mathtran.org/cgi-bin/mathtran?tex=%20a%5Ccdot%20%28-b)
) og
![tex:[[a%5Ccdot%20b]]](http://www.mathtran.org/cgi-bin/mathtran?tex=a%5Ccdot%20b)
, så får du 0 til svar. Vi får dette til ved å bruke den distributive lov (faktorisere ut en felles faktor – i dette tilfellet a):
Dette viser at
![tex:[[a%5Ccdot%28-b%29%3D-a%5Ccdot%20b]]](http://www.mathtran.org/cgi-bin/mathtran?tex=a%5Ccdot%28-b%29%3D-a%5Ccdot%20b)
. La oss så gå videre og se på
![tex:[[%20%28-a%29%28-b%29]]](http://www.mathtran.org/cgi-bin/mathtran?tex=%20%28-a%29%28-b%29)
. Vi vil vise at dette er lik
![tex:[[a%5Ccdot%20b]]](http://www.mathtran.org/cgi-bin/mathtran?tex=a%5Ccdot%20b)
. Det kan vi gjøre ved å vise at
![tex:[[%20%28-a%29%5Ccdot%28-b%29%2B%28-a%5Ccdot%20b%29%3D0]]](http://www.mathtran.org/cgi-bin/mathtran?tex=%20%28-a%29%5Ccdot%28-b%29%2B%28-a%5Ccdot%20b%29%3D0)
. Nå vet vi at andre leddet på venstresiden i dette uttrykket er lik
![tex:[[a%5Ccdot%20%28-b%29]]](http://www.mathtran.org/cgi-bin/mathtran?tex=a%5Ccdot%20%28-b%29)
. Vi får derfor
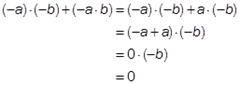
Dette viser at
![tex:[[%28-a%29%5Ccdot%28-b%29%3Da%5Ccdot%20b]]](http://www.mathtran.org/cgi-bin/mathtran?tex=%28-a%29%5Ccdot%28-b%29%3Da%5Ccdot%20b)
.
Mitt poeng med dette blogginnlegget er å vise et eksempel på at matematikk er mer enn å kunne memorere ulike definisjoner og regler. For meg er det viktig at elevene får oppdage alle sidene med faget, ikke bare de aller flinkeste i for eksempel R2. Jeg er litt redd for at faget i dag er delt opp etter skoleslag. På barnetrinnet er det mer oppdagende aktiviteter og lite innslag av den formelle siden ved faget mens i videregående er mer regler og algoritmer og litt av den formelle siden. Alle sidene må jobbes med på alle nivå —også på universitet og høgskole.
og
.
. Denne verdien var litt høyere enn observert måling. Årsaken til denne «feilen» er at været påvirker tidevannet. I dette tilfellet var det hele 24 cm lavere vannstand enn modellene brukt av sjøkartverket. En slik vurdering av modellen hører selvsagt med til modelleringskompetansen til elevene.