Modellus – tips til Fysikkundervisningen!

I Fysikk 1 og 2 i videregående skole er et av hovedområdene å kunne beskrive naturen med matematikk. For Fysikk 2 blir dette beskrevet slik:

Hovedområdet handler om hvordan matematikk blir brukt som språk i fysikk, ved bruk av vektorregning, differensialregning og integralregning. Matematikken som grunnlag for å modellere og gjøre beregninger ved hjelp av datamaskiner og vurdere modellers gyldighet er sentralt i hovedområdet.

Det er min erfaring at denne koblingen mellom matematikk og fysikk kan falle mange elever tungt. Det kan lett bli komplisert når vi skal beskrive naturen. I dette innlegget vil jeg ta et eksempel fra mekanikken og jeg vil se hvorda vi kan briuke programmet Modellus til å løse problemet.

Vi skal se på en partikkel som faller i tyngdefeltet. Denne gangen skal vi ikke se bort fra luftmotstanden, men sette opp en matematisk modell for denne. Det er to alternativer som peker seg ut. Det ene er et luftmotstanden L er proporsjonal med farten

$$ L=k\cdot v$$

Dette gir en god modell når farten en liten. Dersom dette ikke er tilfellet, så kan følgende være en bedre modell:

$$L=k\cdot v^2$$

Problemet med denne modellen er at den gir en komplisert ikke-lineær differensiallikning, mens den første gir en differensiallikning som elever i R2 når skal kunne løse. Det er her Modellus kommer inn. Dette programmet består av flere vinduer, ett hvor vi skriver inn modellen, et grafvindu, et tabellvindu og et tegnefelt.

I vinduet med den matematiske modellen skriver vi inn alt vi trenger. I dette tilfellet vi det si å sette opp Newtons 2. lov:

På en måte vil jeg si at det er dette som er utfordringen sett fra en fysikklærers ståsted. Her må en passe på at en ikke bruker bevegelsesformlene som elevene har jobbet så mye med. Hvorfor? Fordi disse forutsetter konstant akselerasjon, noe som ikke er tilfelle her. En annen ting er at alle variabler må defineres. I modellen for luftmotstanden inngår farten v. Derfor må denne spesifiseres som den deriverte til s.  Videre må sammenhengen mellom fart og akselerasjon settes opp (siste likning). Dette er sammenhenger som programmet ikke kjenner til og som vi må mate inn.

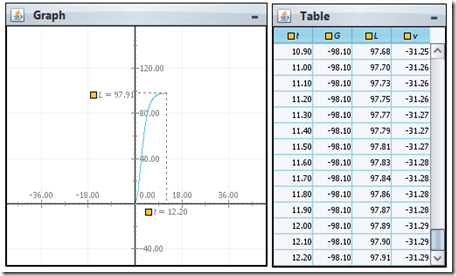
Det fine med Modellus er at du kan teste modellen på et objekt i tegnefeltet. Nedenfor ser du en animasjon av en slik test av akkurat denne modellen. I dette tilfellet er k=0,1 og massen lik 10 kg.

I følge denne modellen vil farten gå mot ca 31 m/s. Vi ser også at G og L etter hvert blir like store.

 

Under panseret ligger det masse numeriske beregninger som ville være alt for avanserte for en elev i videregående. Men selve modellene er innenfor det vi kan forvente av en elev å forstå.